しかし、コンデンサが交流ならば通してくれるということであっても、残念ながら、どの周波数も平等に通してくれるかというと決してそうではないことは、もうご存知のとおりです。本章では、コンデンサのような周波数によって伝達特性の異なる素子の性質や、アンプの設計bにおける計算方法等について説明してみたいと思います。
コンデンサのリアクタンス
コンデンサは、直流は通さない、交流は通す、という性質を持っています。いいかえると、直流的には絶縁体で、交流的には抵抗器かまたはほとんど導線のような性質を持っていると考えてもいいでしょう。(注:実際には、コンデンサは種類によっては絶縁体とはいえないような性質を持つものもあります。)では、交流をどれくらい通すのかというと、0.1μF(マイクロ・ファラッド)のコンデンサの場合、100Hzで約16kΩ、1kHzで約1.6kΩ、10kHzで約160Ωの抵抗と同じになります。このように周波数が低いほど抵抗値(コンデンサのリアクタンスという)が高くなり、その度合いは周波数に反比例し、周波数が10倍になると、コンデンサのリアクタンスは10分の1になります。これが100μFのコンデンサの場合ですと、100Hzで約16Ω、1kHzで約1.6Ω、10kHzで約0.16Ωのはずです。このようにコンデンサの容量が大きいほど、リアクタンスが低くなり、その度合いはコンデンサの容量に反比例します。(注:実際には、周波数とコンデンサのリアクタンスの関係は完全な反比例ではなく、周波数をどんどん高くしていった時に、限りなくゼロになるかというと、そうではありません。ある周波数では横ばいになり、それよりも高い周波数では逆に上昇しはじめます。アルミ電解コンデンサの場合は、100Hz以下の低い周波数でも計算通りの特性にはなりません。)
さまざまな値のコンデンサが、いろいろな周波数でどの程度のリアクタンスを持っているのかを、おおよそ知っているということは、アンプを設計する場合にとても役にたちます。この後、リアクタンスの計算法をご紹介しますが、桁の取り方を結構間違えやすいのです。そんなとき、音楽でいう絶対音感のような基準を知っていれば、計算の時に桁どりでミスをすることがなくなります。
| 10Hz | 100Hz | 1kHz | 10kHz | 100kHz | |
|---|---|---|---|---|---|
| 100pF | --- | 16MΩ | 1.6MΩ | 160kΩ | 16kΩ |
| 0.001μF | 16MΩ | 1.6MΩ | 160kΩ | 16kΩ | 1.6kΩ |
| 0.01μF | 1.6MΩ | 160kΩ | 16kΩ | 1.6kΩ | 160Ω |
| 0.1μF | 160kΩ | 16kΩ | 1.6kΩ | 160Ω | 16Ω |
| 1μF | 16kΩ | 1.6kΩ | 160Ω | 16Ω | 1.6Ω |
| 10μF | 1.6kΩ | 160Ω | 16Ω | 1.6Ω | 0.16Ω |
| 100μF | 160Ω | 16Ω | 1.6Ω | 0.16Ω | --- |
| 1000μF | 16Ω | 1.6Ω | 0.16Ω | --- | --- |
| 10000μF | 1.6Ω | 0.16Ω | --- | --- | --- |
注:「---」の部分は、コンデンサ素子の性質上計算どおりの信頼できる値にならない領域です。
これを公式にすると、以下のようになります。
R = 1 / ( 2πfC )
しかし、これでは(私の場合)ちょっと使いにくいので、この式を実用的な形に書き換えたのが下の式です。
R(kΩ) = 159 / { f(Hz) × C(μF) }・・・式1
この式を変形すると、リアクタンス値とコンデンサ容量値から周波数値を逆算することができます。
f(Hz) = 159 / { R(kΩ) × C(μF) }・・・式2
コンデンサと抵抗との組み合わせ(その1)
さて、ここに0.1μFのコンデンサと47kΩの抵抗による回路があります。(図1)
図1
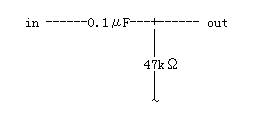
周波数が20Hzの時のこのコンデンサのリアクタンスは上の式1から、160 / (20×0.1) = 80と求まります。つまり、20Hzのときのリアクタンスは、80kΩです。次段の入力インピーダンスは47kΩですから、20Hzでは半分以下に減衰することになりそうです。
このようにして、1Hz〜100kHzまでの帯域について、0.1μFのコンデンサのリアクタンスを計算して、47kΩの抵抗との減衰量を計算してグラフにしてみたのが、図2の赤い曲線です。-6dB(1/2の減衰)のポイントは34Hzです。この34Hzという値は、上の式2で求めた値と同じになります。
図2
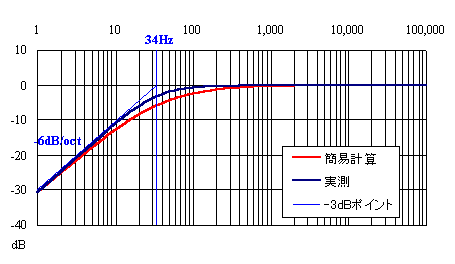
次に、実際にこの回路を組んでオシレータとミリバルを使って測定したみた結果が、図2の青い曲線です。この場合、34Hzでの減衰は-3dBしかなく、計算値の-6dBとは食い違っています。なぜでしょうか?
このことをきちんと理解するには、どうしても位相の性質を知らなければなりません。しかし、電子回路における位相回転(進・遅)について正確に理解するというのは、結構骨の折れる勉強です。そこで、本章では位相の問題については思い切って省略することにします。(基準特性と位相の性質について詳細に勉強したい方は、百瀬了介著「真空管アンプ完全設計法」ラジオ技術社等の文献を参考にしてください。)
「ここでは、もっと現実的に考えて、アマチュアがアンプを設計できる必要最小限の実用的な知識にとどめたいと思います。どう考えたらいいかというと、図2の赤・青それぞれの曲線は、おおむね似ており、その誤差は最大で3dBでしかないこと。しかも、基準周波数(図2の場合は34Hz)から離れれば離れるほどその誤差は無視できるくらい僅少になってゆくということです。第三者に対して正確な説明をする場合はともかくとして、自分自身のアンプの設計の範囲であれば、位相のことを考えない簡易計算(すなわち赤い曲線)でも充分であるということです。式2で求めた基準周波数においては、簡易計算法では-6dBとなりますが、実際は-3dBなのだ、ということだけ心の中に留めておけばいいのです。」・ ・・・・重要
さて、コンデンサ1個と抵抗1本の減衰回路では、基準周波数を起点として、それよりも低い周波数ではどんどん減衰してゆき、その傾きは「周波数が半分になるごとに、利得も半分になる」ような性質を持っています。このことを「-6dB/oct」と表現します。1オクターブごとに6dB減衰するからです。周波数が1/10になれば、利得も1/10(つまり-20dB)です。図2では、3.4Hzのときのレスポンスがだいたい-20dBになっているでしょう。ですから0.34Hzでは、-40dBであると計算できます。ほとんど暗算でいけますね。
この計算は、増幅回路の低域特性の計算だけではなく、トーンコントロールの計算、電源のリプル(50Hzあるいは100Hz)のフィルタ回路にも同様に適用できます。
コンデンサと抵抗との組み合わせ(その2)
今度は、47kΩの抵抗と0.001μFのコンデンサとによる回路です。(図3)
図3
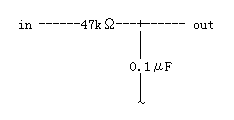
図1の回路と比べると抵抗とコンデンサの位置が反対になっていますが、これまでと同じように周波数ごとのコンデンサのリアクタンスを計算で求め、位相のことは考えずにこれを単純に抵抗であると思って減衰利得を計算して、グラフにしてみたのが図4です。
図4
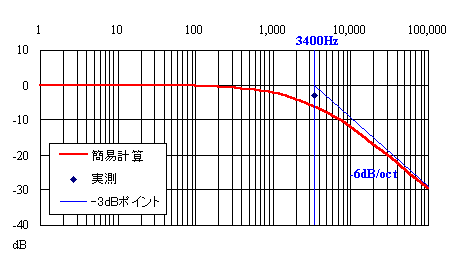
今度は、高域にゆくにつれて減衰量が大きくなるような結果になっています。そして、-3dBとなる基準周波数は3400Hzとなって、式2による計算で求めた値と同じになります。
コンデンサと抵抗との組み合わせ(その3)
今度は、1kΩの抵抗と10μFのコンデンサとによる回路です。この回路では、コンデンサと抵抗が並列になっています。真空管増幅回路のカソードにこのような回路がよく使われますね。(図5)
図5
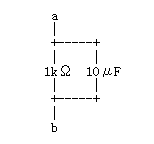
ここでは、並列になった抵抗とコンデンサの並列合成値を求めて、グラフにしてみたのが図6です。34Hzを境に特性が切り替わります。カソード回路の場合は、34Hz以下の周波数では利得が若干低下します。
図6
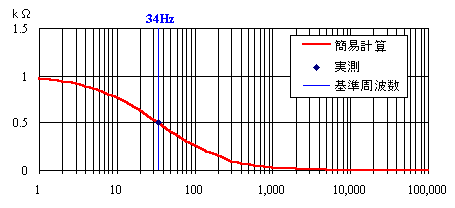
充分高い周波数では、コンデンサのリアクタンスがゼロに近づくために、並列合成値もゼロに収束してゆき、反対に低い周波数では抵抗値1kΩに収束してゆきます。赤い色の曲線はあくまで簡易計算法によるもので、実際の曲線はこれよりもわずかにきついカーブになります。しかし、この程度でもかなり正確な解析ができますし、アンプ設計を進める上で全くといっていいくらい不便はありません。
