定電圧回路とは
「定電圧回路」とは、その回路に流れる電流の大小にかかわらず、その両端につねに一定の電圧を生じさせる回路のことです。理想的な定電圧回路では、その回路に流れる電流が変化しても、その両端に生じる電圧の変化量はゼロです。そのため、動作中の定電圧回路は交流的な内部抵抗も(理想的には)ゼロになります。電源電圧等の外部環境の影響を受けることなく一定の電圧が必要な場合や、直流電圧は一定値を保ちたいが、信号はバイパスさせたいような場合に非常に便利です。
定電圧回路のこのような性質は、増幅回路では、安定した電圧が必要な電源回路や、一定以上高い電圧にならないような保護回路や、前章でご紹介した定電流回路の一部品等、じつにさまざまな用途で利用されます。
定電圧回路・・ツェナ・ダイオード(ZD)
定電流回路・・定電圧放電管
。
定電圧回路・・ツェナ・ダイオード+トランジスタ
。
定電流「的」回路・・3極管+抵抗
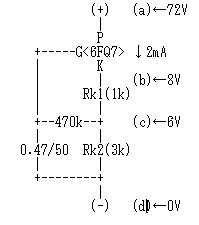右の回路を見てください。(a)〜(d)間に72Vの電圧がかかっており、そこには2mAの電流が流れています。もし、(a)〜(c)間が1本の抵抗だったら、その値は、72V÷2mA=36kΩのはずですね。この回路の直流動作を考えてみます。(a)〜(c)間に限っていえば、これは1kΩのカソード抵抗を持ったごく普通のカソードバイアス回路です。もし、(a)〜(c)間が1本の抵抗だったら、その値は、66V÷2mA=33kΩのはずです。(a)〜(c)間は2端子回路ですが、これは、
抵抗値 = rp(=内部抵抗) + Rk × ( μ + 1 )
で求めることができます。rp=約10kΩ、μ=約22、Rk1=1kΩを代入して計算すると、
33kΩ = 10kΩ + 1kΩ × ( 22 + 1 )
抵抗値は、33kΩとなって抵抗とみなした時の値ときれいに一致します。これに直列になっているRk2の3kΩをたして36kΩとなります。では交流的にみた場合はどうなるでしょうか。コンデンサ(0.47μF)が生きてますから、rp=約10kΩ、μ=約22、Rk1=1kΩ+3kΩになります。そこで、これを代入して計算すると、
102kΩ = 10kΩ + 4kΩ × ( 22 + 1 )
抵抗値は、102kΩとなりました。このような回路では、直流的には36kΩの抵抗と等価なのに、交流的には102kΩの抵抗と等価になります。つまり、交流的には、不充分ながらも定電流(的?)回路となるのです。
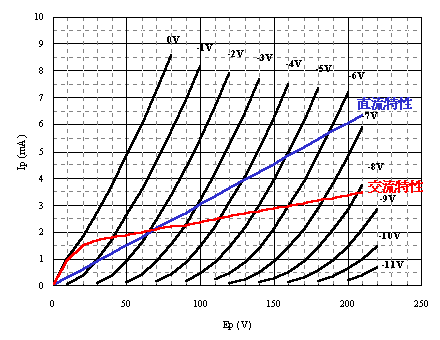
このような動作をEp-Ip特性上で表現したのが右図です。直流特性(青線)は、カソード抵抗値=1kΩの2端子回路の特性ですので、Ip=1mAの時のバイアスは-1V、Ip=2mAの時のバイアスは-2Vとなるような点を結んでいます。交流特性(赤線)は、バイアスが0Vの時の立ちあがり曲線と、Ep=66V、Ip=2mAのポイントで青線と交差するような102kΩの角度を持った直線との合成です。
この赤い線が、定電流「的」回路の特性にあたるわけですが、角度がついていることに目をつぶれば、定電流特性「的」な特徴を持っていることがよくわかります。Rk2の値をもっと大きくすれば、より定電流特性「的」になってゆきます。
SRPP回路の応用で、μフォロワと呼ばれる回路がありますが、μフォロワ回路ではこの定電流(的?)回路をプレート側の負荷として活用しているために、通常の増幅回路よりも高い利得が得られるのです。
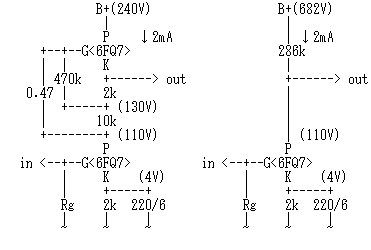
右図(左)の例では、もっぱら増幅作用を営んでいる下側の6FQ7は、Ep=106V、Ip=2mAでバイアス=-4Vの動作になっています。上側6FQ7はここでご紹介した定電流「的」回路になっていて、その2端子回路としての交流インピーダンスは、
286kΩ = 10kΩ + 12kΩ × ( 22 + 1 )
となりますので、下側管からみたら、動作条件は右図(右)と等価になります。上側管の動作条件はさておき、増幅作用の源泉である下側管の動作としては、定電流「的」負荷が与えられた場合の動作はこういうことになるわけです。
補足しますと、μフォロワ回路では、下側管のプレートに生じた出力は、コンデンサ(0.47μF)を通って上側管グリッドに入力されます。一方で、出力は上側管カソードから取り出されているため、カソード・フォロワと同じ効果が生じ、最終的な出力インピーダンスは非常に低くなります。上側管のグリッドに入力があるとすると、下側管からみたプレート負荷は286kΩ一定というわけにはゆかず、変動するのではないか、と考えたくなります。しかし、よく考えてみてください。なぜ、下側管からみたプレート負荷は286kΩのままほとんど一定になるのか。これは、皆さんへの応用問題としての宿題です。
定電流回路・・トランジスタ
トランジスタは、単独では定電流特性を持っていませんので、他の素子と組み合わせることで定電流特性を実現します。回路が若干複雑になりますが、回路を工夫することで、高い精度、すぐれた温度安定性、高い耐圧、広範な電流特性を得ることができます。
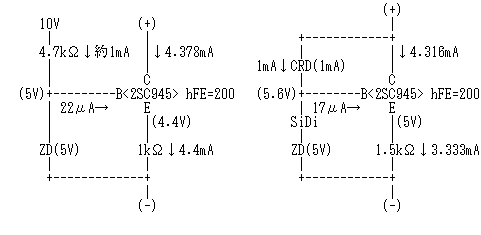右図の左の回路が、トランジスタを使ったもっともベーシックな定電流回路です。トランジスタには、NEC製のロングセラー、2SC945を使ってみました。2SC945のhFEはおおよそ200ですから、コレクタ電流が1mAの時のベース電流は、1mA÷200=5μAになります。
外部から+10V、約1mAの電源を供給し、これで5Vのツェナーダイオード(ZD)を動作させます。トランジスタのエミッタ側には、抵抗がはいっています。トランジスタのベース〜エミッタ電圧は、ほぼ0.6Vで一定とみなせますから、この抵抗の両端には、5V-0.6V=4.4Vの電圧がかかる計算になります。もし、この抵抗値が1kΩであれば、この抵抗には、4.4V÷1kΩ=4.4mAの電流が流れます。コレクタ電流は、エミッタ電流からベース電流を引いた値ですから、この回路では4.378mAの定電流回路になります。
半導体のほとんどすべては、温度依存性を持っています。ツェナーダイオードは、5Vあたりでは温度変化に対しておおむねニュートラルですが、6V以上になると温度変化に対して正の相関が現れはじめるため、温度が上昇するとともにツェナー電圧も上昇します。たとえば、10Vのツェナーダイオードでは温度1℃あたり+0.06%くらいありますから、1℃の上昇で+6mV、50℃の上昇では+0.06Vになります。反対に、トランジスタのベース〜エミッタ間電圧やシリコンダイオードの順方向電圧は、温度に対して負の相関があり、その値は温度1℃あたり-2mVです。これは、温度1℃あたり-0.33%に相当しますからばかにできません。
温度に対する安定度という点で考えると、上図左の回路はちょっと問題があります。ツェナーダイオードは5Vのものを使っていますので、温度依存性はないものとします。しかし、トランジスタのベース〜エミッタ間電圧は温度が高くなるにつれて低下するため、温度が50℃上昇した場合、-2mV×50℃=-0.1Vの低下が生じて、1kΩの抵抗の両端電圧は、4.4Vから4.5Vに上昇することになります。真空管アンプのシャーシ内部は、50℃の温度上昇くらいは日常茶飯事だということを忘れてはいけません。
この温度依存性を打ち消す操作のことを「温度補償」といいます。上図右の回路は、ツェナーダイオード(ZD)と直列にシリコンダイオード(SiDi)を入れることで、トランジスタ(2SC945)のベース〜エミッタ間電圧の温度依存性をきれいに打ち消しています。また、ツェナーダイオード側の電源供給も、定電流側から取って自己完結型とすることで別立ての電源(+10V)を不要にしています。
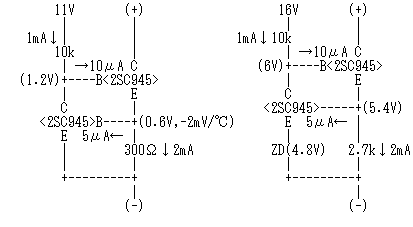上記の定電流回路にトランジスタをもう1つ追加して、定電流特性を飛躍的に向上させ、回路インピーダンスがきわめて高くなっているのが右図の2つの回路です。
左側の回路では、ツェナーダイオードを省略したため、非常に低い動作電圧(1V以下)で稼動し、しかも、非常に高い回路インピーダンスが得られます。一方で、トランジスタのベース〜エミッタ間電圧の温度依存性(-2mV/℃)がそのまま定電流特性まで現れてきます(-6.7μA/℃)から、周囲温度が30℃上昇した場合、2mAから2.2mAまで増加します。
右側の回路では、ツェナーダイオードを追加することで、温度に対する安定度はほぼ理想的なところまで追いこんでいる反面、6V以上でないと正常な定電流特性は得られません。
いずれの場合も、2SC945を、もっと耐圧の高いトランジスタに置き換えたり、放熱板を取り付けたパワートランジスタにすることによって、自在に高電圧・大電流化できるところがこの方式の良い点です。